Statistical Guide to loss functions 🚧
A different perspective on loss functions using Statistical Learning Theory
Under construction! 🚧
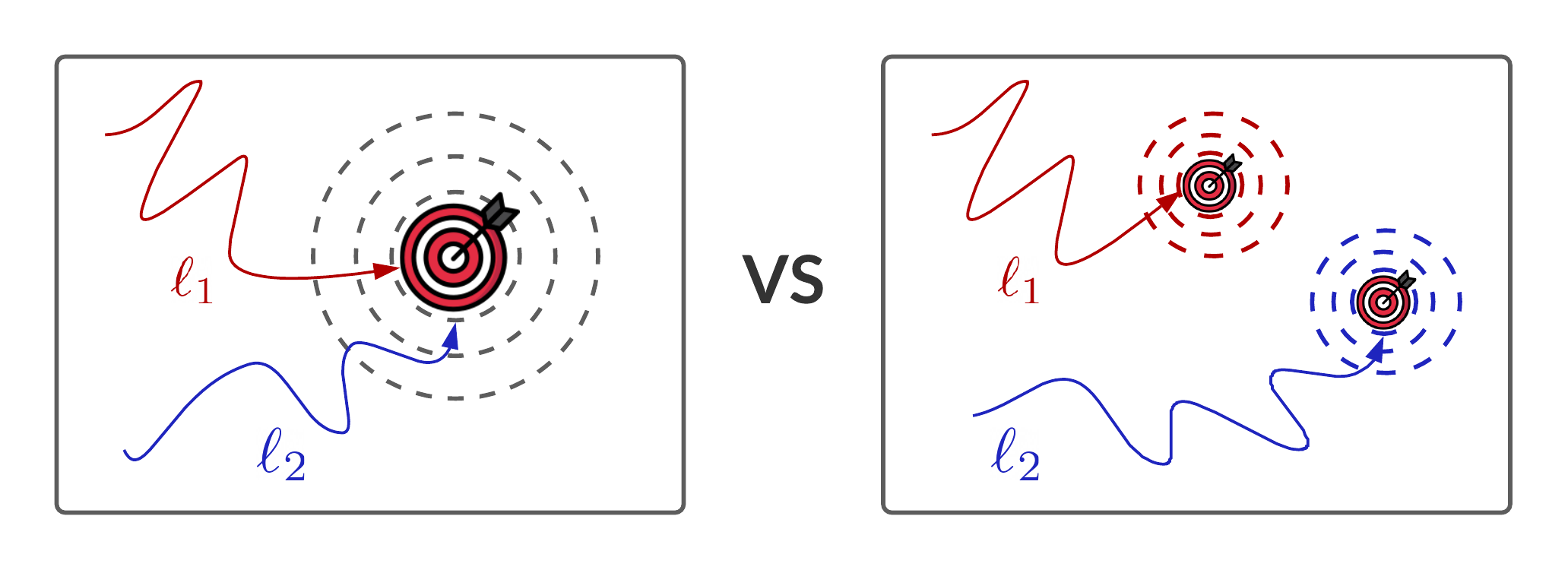
Often in practice, we are see a variety of loss functions in different domains. Intuitively, we may erroneously think (atleast I did) of them as computationally different ways of arriving at the same target.

For example in a vanilla regression problem given $f(x)$ to be our estimate function and $y$ to be the true value, consider two loss functions: \[\ell_1(f(x),y) = (f(x) - y)^2 \quad \text{ and } \quad \ell_2(f(x),y) = |f(x) - y|\]
What is the advantage of choosing one over the other? In a “hand-wavy” sense both penalize our estimate when it is away from the true value, so it feels natural to assume that both lead our estimate towards the same optimal target. Although the optimization dynamics of both loss functions maybe different, they must be yielding the same end result (minimizer) right? Well not quite!